En este post vas a aprender qué es la teoría de conjuntos en matemáticas discretas desde cero, explicado paso a paso y con múltiples recursos.
La teoría de conjuntos te va a servir mucho, ya sea que estudies ingeniería en sistemas o en programación, ya que te permite tener fuertes bases y fundamentos sobre cómo resolver problemas de operar con grupos de elementos y sus relaciones, algo común en el desarrollo de software o programación.
De hecho, en algunos lenguajes de programación son un tipo de estructura de datos (Set).
const mySet1 = new Set()
mySet1.add(1) // Set [ 1 ]
mySet1.add(5) // Set [ 1, 5 ]
mySet1.add(5) // Set [ 1, 5 ]
mySet1.add('algún texto') // Set [ 1, 5, 'algún texto' ]Este es un ejemplo de un conjunto en el lenguaje JavaScript por parte de Mozilla.org.
Qué es un conjunto en matemáticas discretas
Un conjunto en matemáticas discretas es un grupo de elementos únicos e irrepetibles, que pueden ser finitos o infinitos y cuyos elementos pueden ser cualquier valor como números, letras, e incluso, objetos del mundo real.
Otra definición puede ser:
Un conjunto es la reunión en un todo de objetos de nuestra intuición o de nuestro pensar, bien determinados y diferenciables los unos de los otros.
Georg Cantor (1845-1918)
Por ejemplo, podemos decir que las letras del abecedario son un conjunto porque cada letra es única, irrepetible y bien diferenciada una de otra.
Determinación de un conjunto por extensión o comprensión
Básicamente, la determinación de un conjunto puede ser por extensión o por comprensión.
Ejemplo de determinación de un conjunto por extensión.
Un conjunto por extensión se determina enlistando uno a uno todos los elementos que lo conforman, separados por coma. Los siguientes ejemplos son conjuntos por extensión.
A = {vocales}
B = {a, e, i, o, u}Ejemplo de determinación de un conjunto por comprensión o forma constructiva.
La determinación de un conjunto por comprensión o forma constructiva consiste establecer una condición o propiedades que deben cumplir cada elemento del conjunto, por ejemplo:
A = {v | v es una vocal}
B = {n | n es un número natural menor que 10}El símbolo | se lee como “tal que”, o sea, el conjunto A es igual al elemento “v” tal que el elemento (s) “v” es una vocal.
Como puedes ver, ya no colocamos la lista de los elementos sino que colocamos una condición que deben cumplir, esto es especialmente útil cuando queremos expresar conjuntos que tienen tantos elementos que sería impráctico enlistarlos uno a uno.
Teoria de conjuntos diagrama de venn
Para ejemplos gráficos, en teoría de conjuntos se utilizan los diagramas de Venn para representar conjuntos, lo que puede ayudar a comprender mejor lo que es la teoría de conjuntos en matemáticas. Un ejemplo de diagrama de Venn es:
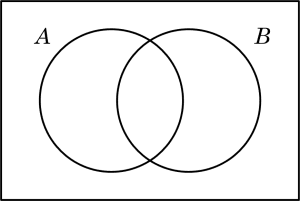
Mariano Deheza, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons
Donde el conjunto A es el círculo de la izquierda, el conjunto B el de la derecha, y la parte de en medio donde se combinan, representa los elementos que están en común entre A y B.
¿De qué te puede servir esto? Pues bien, esto es el fundamento que necesitas saber para resolver ejemplos y ejercicios de teoría de conjuntos.
Relación entre conjuntos y elementos en matemáticas
noción de conjuntos y elementos, relación entre conjuntos y elementos, ejemplos de conjuntos y elementos, diferencia entre conjuntos y elementos
La noción de conjuntos y elementos es más fácil de entender si consideramos que un conjunto está formado por elementos.
Es decir, la diferencia entre conjuntos y elementos es que un elemento es individual que puede formar parte de un conjunto.
Ejemplos de conjuntos y elementos:
A = {1, 2, 3}¿Cuáles son los elementos del conjunto A? la respuesta es: 1, 2 y 3.
Con esto en mento, podemos declarar una relación entre conjuntos y elementos, como “pertenece a” y “no pertenece a”:
A = {1, 2, 3}
1 pertenece a A = 1 ∈ A
4 NO pertenece a A = 4 ∉ AEl símbolo ∉ se lee como “pertenece” y el símbolo ∉ se lee como “no pertenece”. Estos son sólo un ejemplo de simbología de teoría de conjuntos.
Tipos de conjuntos en matemáticas discretas
Podemos clasificar los tipos de conjuntos en matemáticas discretas en base a los elementos que contienen.
- Conjunto Nulo o Vacío. Es un tipo de conjunto especial porque expresa que no contiene ningún valor. Puede representar los símbolos: ∅, o también
{}. - Conjunto Unitario. Es un conjunto que contiene sólo un elemento.
A = {1} - Conjunto Finito e Infinito. Un conjunto finito contiene elementos con un fin, como las vocales del abecedario. Un conjunto infinito contiene elementos sin fin, como los números naturales.
- Conjunto Disjuntos. Son conjuntos que no tienen elementos en común o ninguna relación.
- Conjunto Juntos. Son conjuntos que sí tienen elementos en común o una relación.
- Subconjunto de un conjunto. Un conjunto puede como elemento a otro conjunto que llamamos subconjunto.
- Conjunto Potencia o Potencia de un Conjunto. Es un conjunto que contiene a todos los subconjuntos de un conjunto original.
- Conjunto Universal o universo (U). Es un tipo de conjunto especial que representa a todos los elemento existentes en un contexto dado. Por ejemplo, el universo puede ser todos los números naturales y por dentro, podemos tener un conjunto
A = {1, 2, 3}, en este caso, el universo representa todos los números naturales faltantes que no tiene el conjunto A.
Diagramas de Venn y SQL
Es muy probable que en tu carrera como desarrollador de software necesites usar bases de datos relacionales.
Un truco para comprender las instrucciones para relacionar tablas de datos son los diagramas de Venn
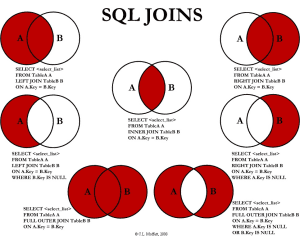
Aunque esto es un ejemplo visual muy ilustrativo, también hay quienes consideran que es más adecuado utilizar otro tipo de diagramas para representar uniones y relaciones porque no son una analogía 100% fidedigna.
Por ejemplo, un JOIN no es estrictamente una operación de un conjunto, pero a pesar de ello, usar diagramas de Venn ayuda mucho como ejemplo visual para comprender las queries de bases de datos.
Si quieres aprender más sobre qué es la teoría de conjuntos en matemáticas discretas, accede a todos los recursos gratuitos que he preparado para ti dando click acá: