Matematicasdiscretas.org nace para difundir recursos fáciles de entender y orientados a estudiantes de ingeniería en sistemas y programadores que quieran lograr pasar al siguiente nivel por medio de matemáticas discretas para programación.
Ya sea que estés estudiando una ingeniería en sistemas computacionales o que seas un programador autodidacta, te invito a que descubras cómo puedes ser mejor profesional con los siguientes ejemplos de las matemáticas discretas que verás a continuación.
Ejemplos de Matemáticas Discretas en programación
Por cierto, si lo deseas, te invito a ver este vídeo de introducción a las matemáticas discretas para programación del canal oficial de YouTube:

¿Necesitas saber Matemáticas Discretas para ser programador?
La respuesta es un “depende”.
Si vas a crear desarrollos sencillos como sitios web estáticos, o dinámicos, usando simples CRUD u operaciones que sean muy comunes, es posible que no las requieras del todo.
Pero si vas a participar en proyectos de ingeniería de software más retadores como sucede en las empresas FAANG (Facebook, Apple, Amazon, Netflix, Google), entonces sí que son muy, muy importantes para ti, además de que te vas a diferenciar de un programador promedio (no seas promedio).
Te comparto algunos ejemplos de usos reales donde puedes beneficiarte de este tipo de matemáticas:
- Crear un algoritmo para determinar la ruta más corta entre un punto A y un punto B.
- Determinar la complejidad de un algoritmo y usar ese conocimiento para optimizar y bajar el tiempo de ejecución de segundos a fracciones de segundos.
- Determinar las relaciones entre colecciones de datos para saber qué elementos hay en común, o que son distintos.
- Crear código con expresiones lógicas usando técnicas como tablas de verdad o proposiciones lógicas (veremos más sobre ello).
- Crear un algoritmo para conocer las diferentes combinaciones posibles que puedes tener en un listado de valores.
Existen N maneras de resolver un mismo problema, pero nosotros como ingenieros de software necesitamos ser conscientes de que siempre puede existir una manera mejor y buscarla cuando sea prudente hacerlo.
Guía de estudio de Matemáticas discretas
A continuación te comparto un temario ordenado que puedes usar como guía para estudiar.
- Sistemas numéricos. Comprende los fundamentos de los diferentes sistemas de numeración que vas a utilizar a partir de este momento. Debido a que tienen una fuerte relación con las ciencias de la computación, es recomendado que inicies primero con este tema.
- Teoría de conjuntos. Aprende sobre cómo expresar relaciones entre colecciones de datos, un tema relacionado con esta estructura de datos que incluso existe en algunos lenguajes de programación.
- Lógica proposicional. La lógica de programación la vas a aplicar independiente del lenguaje que elijas aprender, por lo que tener bases de lógica proposicional te va a ayudar a fortalecer bastante tu lógica a la hora de crear programas.
- Teoría de grafos. Esta es otra estructura de datos que puedes usar para solucionar problemas reales expresando datos por medio de grafos, esto puede marcar la diferencia entre usar una solución u otra diferente a grafos.
Veamos más a detalle sobre cada área.
Matemáticas discretas y sistemas numéricos
Las computadoras a un bajo nivel utilizan código binario para almacenar información y ejecutar instrucciones.
Pero ¿Qué es el código binario y cómo me puede servir ese conocimiento como programador? Da click en el siguiente post donde te hablo más a detalle.

Cómo PASAR de BINARIO a OCTAL Fácil y Rápido

Cómo pasar de OCTAL a BINARIO Paso a Paso

Cómo pasar de DECIMAL a BINARIO paso a paso

Cómo convertir de BINARIO a DECIMAL fácil paso a paso

Sistemas numéricos en Matemáticas Discretas 2024
Qué es la Teoría de conjuntos
Si eres programador, conocer de conjuntos y subconjuntos de matemáticas discretas te va a ayudar a tener fuertes bases y fundamentos sobre cómo operar con grupos de elementos de manera correcta, pues esta rama de las matemáticas estudia colecciones o grupos de elementos contables y las relaciones entre ellos.
Da click en los siguientes posts para ver más información.

Qué es la teoría de conjuntos en matemáticas discretas
Simbología de Teoría de conjuntos

Teoría de conjuntos con ejemplos
Qué es la lógica proposicional
La lógica proposicional es una rama de las matemáticas que estudia enunciados que se les puede representar con símbolos y nos ayuda a definir pruebas o demostraciones de verdad o falsedad sobre los mismos.
Este tema es el que más probablemente te va a ayudar a mejorar tu lógica de programación, porque te ayuda a hilar y expresar mejor tus ideas, lo que es esencial para crear un código de mejor calidad.
Por ejemplo, en tu día a día como programador vas a requerir hacer expresiones condicionales o booleanas para tomar decisiones:
- SI la edad es mayor o igual que 18, entonces es mayor de edad.
- Si el usuario no existe, entonces regresar mensaje de error.
- Si “esto”, entonces “haz esto”.
Para esto te pueden ayudar las famosas tablas de verdad que consisten en una manera de comparar diferentes combinaciones de expresiones de verdadero y falso usando conectores lógicos:
- Conjunción: Representado como “Y”, la proposición compuesta es verdad si las dos proposiciones simples son verdaderas. if (true && true).
- Disyunción: Representado con la letra “O”, la proposición compuesta es verdad sólo si UNA de las dos proposiciones es verdadera. (if true || false).
- Negación: Representado con la expresión “no” o “no es cierto que”, asigna lo contrario de la proposición. if (!false) o if (!true).
Existe mucho más tela de dónde cortar para este tema, pero con lo anterior ya tienes una mejor idea de qué trata la lógica proposicional.
Qué es la Teoría de grafos
La teoría de grafos es de gran interés para ti como desarrollador porque es una rama de las matemáticas y ciencia de la computación que se utiliza para resolver problemas como:
- Optimización de recorridos.
- Algoritmos de búsqueda.
- Análisis de redes.
Por ejemplo, cuando usas Google Maps o Uber para encontrar el camino más corto entre el punto A y punto B (puede considerarse como el “problema del viajero”), o la manera de estructurar una aplicación de red social como Twitter.
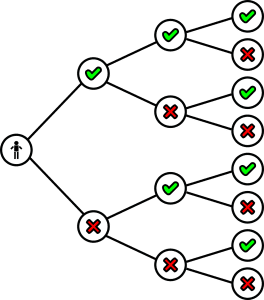
No es estrictamente necesario que dediques todos tus esfuerzos en aprender este tema, pero si tienes las bases mínimas necesarias, te puede ayudar a tener un “ajá!” cuando pienses en la solución de un problema.
Hay cosas que no puedes saber si las vas a aplicar o no, hasta que las conoces.
Claro que para hacer un CRUD típico (Create, Read, Update, Delete) de una aplicación o un sitio web sencillo, puede que no lo necesites, pero para resolver problemas más complejos, sí que te servirá. Pregúntale a un ingeniero de software de Uber.
Incluso este suele ser un tema de entrevistas técnicas para empresas de gran renombre como Google y Amazon.
Qué son las matemáticas discretas
Las matemáticas discretas pueden considerarse como una rama de las matemáticas que abarcan diferentes temas que se relacionan con las ciencias de la computación y que se enfocan en todo aquello que “puede ser contado por separado”, ya sean elementos finitos o infinitos.
¿Qué? 😳
No te preocupes si lo anterior no tuvo mucho sentido, es normal que al inicio suene muy complejo, pero conforme vas repitiendo y entrando en materia, las cosas se vuelven más sencillas.
Si separamos “matemáticas discretas”, tenemos:
- Matemáticas: Ciencia que estudia a los números y sus relaciones.
- Discreto: Como adjetivo, significa separado, distinto.
Podemos afirmar que matemáticas discretas = números o elementos que son separados y distintos.

Ejemplos de matemáticas discretas en la vida cotidiana
Por ejemplo, puedes identificar la hora de un reloj digital como: 13:02 horas, y luego cambiará a 13:03 horas, y así continuamente minuto a minuto.
Puedes considerar que estás viendo una hora discreta porque estás viendo por separado cada minuto, sin ver el tiempo que transcurre en segundos o mili segundos o millares de segundos.
Si ves un reloj analógico (con manecillas), entonces vas a ver, por ejemplo: 13:02:00, 13:02:01, etc. y si hacemos un acercamiento, podemos ver 13:02:000001, 13:02:000002, etc, e ir agregando infinitos ceros a la derecha.
Esto puede considerarse lo contrario a discreto, porque ahora estamos viendo una transición continua del tiempo.
¿Quieres saber más de matemáticas discretas y su relación con el desarrollo de software?
También te invito a que te suscribas al canal oficial de YouTube Matemáticas Discretas para programación.