En este post de teoría de conjuntos ejemplos resueltos paso a paso vas a aprender de ejercicios y soluciones con explicaciones al detalle, útil principalmente si estás cursando matemáticas discretas en la ingeniería en sistemas computacionales o si eres un ingeniero de software.
Teoría de conjuntos ejemplos resueltos paso a paso de básico a avanzado
A continuación veremos ejercicios de representación de conjuntos con símbolos, empezando con lo más básico a lo más complejo.
Antes de iniciar, recordemos ¿Qué es un conjunto en matemáticas discretas?
Un conjunto en matemáticas discretas es un grupo de elementos individuales, que pueden ser finitos (con un fin) o infinitos. Por ejemplo, ¿Cuáles son las vocales del abecedario? son: a, e, i, o, u, esto puede ser un conjunto.
Recuerda que la teoría de conjuntos es parte de las matemáticas discretas, un área importante en sistemas computacionales y ciencias de la computación.
Si quieres profundizar más, te recomiendo que des click al post sobre definición de teoría de conjuntos:
Ejemplos de Teoría de Conjuntos
Ejemplo 1: ¿Cómo se representa un conjunto?
Respuesta: Los conjuntos se representan simbólicamente con asignaciones a letras y colocando los valores entre llaves. Por ejemplo, si queremos hacer un conjunto de los números 1, 2 y 3.
A = {1, 2, 3} Nota: Asignamos A pero puedes elegir otra letra según lo requieras.
Los valores que tiene un conjunto se le llaman elementos y normalmente tienen características en común, de modo que son agrupados.
Ejemplo 2: ¿Cómo se representan los días de la semana en un conjunto?
Un conjunto se pueden representar por comprensión o por extensión (numeración):
- Por comprensión. Se describen las características que deben tener los elementos del conjunto.
- Por extensión o numeración. Se enumeran o colocan los elementos del conjunto uno por uno separados por coma.
Ejemplos por comprensión
A = {días de la semana}
A = {d | d es un día de la semana}La segunda manera `A = {d | d es un día de la semana}` se se lee como: El conjunto A es igual a “d” tal que “d” es un día de la semana.
Por extensión o numeración es:
A = {Lunes, Martes, Miércoles, Jueves, Viernes, Sábado, Domingo}Como puedes ver, separamos cada día de la semana, uno por uno separados por coma.
Ejemplo 3: ¿Cómo representar los números naturales en conjuntos?
En matemáticas existe una simbología para representar números. Uno de ellos es “N” que representa los números naturales, los cuáles son todos los números enteros positivos infinitos ya que siempre puede existir un número natural mayor que su antecesor (n = n + 1).
Para expresar los números naturales en la teoría de conjuntos tienes las siguientes opciones:
opción 1: A = {1, 2, 3, 4...}
opción 2: A = {n | n = N}
opción 3: A = {N}La más común es la opción 3 debido a que es la más sencilla pues “N” simboliza por sí mismo a los números naturales, haciendo las opciones 1 y 2 algo redundantes, pero aún así son válidas.
Nota: los tres puntos de la opción 1 indican que sigue para siempre o al infinito.
Ejemplo 4: ¿Cómo representar los números naturales menores a 50?
Ahora vamos a entrar más en materia para definir conjuntos con ciertas características.
A = {n | n ∈ N, n < 50}Se lee: El conjunto de “n” tal que “n” pertenece a los números naturales y que son menores a 50.
Nota: La simbología de `∈` significa “pertenece a”.
Podemos considerar que tenemos dos condiciones separadas por coma. Condición 1: n ∈ N, condición 2: n < 50.
Ejemplo 5: ¿Cómo representar los números naturales impares mayores de 100?
Para representar números impares podemos hacerlo como:
A = {n | n ∈ N, n = 2n -1, n > 100}Se lee como: El conjunto de “n” tal que “n” pertenece a los números naturales, “n” es igual a “n” multiplicado por dos menos uno y “n” sea mayor a 100.
Si lo analizas, la expresión n = 2n -1 es una manera de expresar números impares ya que:
2(1) - 1 = 1
2(2) - 1 = 3
2(3) - 1 = 5
...Recuerda que poner cifras entre paréntesis significa que estamos multiplicando.
Ejemplo 6: Todos los números naturales mayores a cero pero menores a 10.
Ahora vamos a expresar una condición un poco más compleja:
A = {n | n ∈ N, 0 < n < 10}La segunda condición se puede leer como: “n” menor que 10 pero mayor que 0.
Ejemplo 7: Las letras del abecedario y el sub conjunto de las vocales.
Para expresar un subconjunto dentro de un conjunto lo podemos hacer como:
A = {l | l = letras del abecedario, {a, e, i , o, u}}Es válido que un conjunto contenga a su vez un subconjunto, en este caso, podemos afirmar que las vocales son un conjunto que pertenece a su vez al conjunto de las letras del abecedario y lo expresamos como un conjunto interno con sus llaves ({}).
Ejemplo 8: Determinar por extensión el siguiente conjunto.
A = {2n | n ∈ N, 0 < n < 10}Tranquilo, esto puede parecer intimidante a primera vista, pero no te preocupes, a continuación te explico paso a paso cómo resolverlo.
Primero hay que comprender su equivalente en descripción.
Conjunto A es igual a “n” multiplicado por 2 tal que “n” pertenece a los números naturales y es mayor que 0 y menor que 10. Entonces la respuesta es enumerar el listado de números que cumplan esas condiciones y con su multiplicación por 2:
A = {
1 * 2,
2 * 2,
3 * 2,
4 * 2,
5 * 2,
6 * 2,
7 * 2,
8 * 2,
9 * 2
}Por lo tanto, si hacemos las multiplicaciones equivale a: A = {2, 4, 6, 8, 10, 12, 14, 16, 18}. ¿Fue más sencillo de lo que parece, verdad?
Ejemplo 9: Obtener la cardinal de un conjunto dado
Recordemos que la cardinal de un conjunto es igual al número de elementos que componen un conjunto definido.
¿Cuál es la cardinalidad de los siguientes conjuntos?
a): A = {1, 2, 3, 4, 5}
b): A = {n | n ∈ N, 10 <= n <= 20}
c): A = {N}
d): A = {}Respuestas:
- a): la cardinal es igual a 5 porque tiene sólo 5 elementos.
- b): la cardinal es igual a 11 porque: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 son 11 números (observa los signos <= menor o igual que) y pertenecen a los números naturales (N).
- c): la cardinal del conjunto de los números naturales es igual a infinito debido a que ese tipo de números no tienen un fin (n = n + 1).
- d): la cardinal de un conjunto vacío es igual a cero porque no tiene elementos.
Ejemplo 10: Determinar por extensión el siguiente conjunto
A = {n (n + 1) | n ∈ N, 0 < n < 5}Primero hay que comprender lo que expresa. El conjunto A es igual a n multiplicado por n + 1 tal que n pertenece a los números naturales, es mayor que 0 y menor que 5.
Entonces tenemos que n puede ser igual a: 1, 2, 3 y 4 porque es menor que, no menor e igual que. Ahora sólo debemos reemplazar n por esos valores y aplicar la fórmula. Por ejemplo:
si n = 1 entonces: 1 (1 + 1) = 1 (2) = 2.
si n = 2 entonces: 2 (2 + 1) = 2 (3) = 6.
si n = 3 entonces: 3 (3 + 1) = 3 (4) = 12.
si n = 4 entonces: 4 (4 + 1) = 4 (5) = 20.Por lo tanto, el conjunto equivalente expresado con la extensión o numeración es:
A = {2, 6, 12, 20}Nota: Por lo tanto, podemos afirmar que:
A = {n (n + 1) | n ∈ N, 0 < n < 5}
B = {2, 6, 12, 20}
A = BSon conjuntos idénticos porque contienen los mismos elementos.
Teoría de conjuntos ejemplos de Relación de Pertenencia (∈) y no Pertenencia (∉)
Ejemplo de pertenencia
En teoría de conjuntos, la pertenencia (∈) significa que un elemento pertenece a un conjunto dado, por ejemplo: El conjunto A = {1, 2, 3}, entonces 1 ∈ A (uno pertenece al conjunto A) y lo contrario, 10 ∉ A (10 no pertenece al conjunto A).
Dado el siguiente conjunto:
A = {x | x ∈ N, 0 < x < 5}Determina cuál de las siguientes opciones son correctas:
a): 0 ∈ A
b): 5 ∈ A
c): 3 ∈ A
d): 4 ∈ A
e): 5 ∉ A
f): 1 ∉ ALa respuesta es: c, d y e debido a que el 0 y el 5 no pertenecen al conjunto dado que estamos usando el “menor que” y no el “menor e igual que”.
El ejemplo del diagrama de Venn correspondiente a este conjunto es:

Ejemplos de operaciones entre conjuntos (unión , intersección y diferencia) con diagramas de Venn
A continuación veremos teoría de conjuntos ejemplos resueltos paso a paso con diagramas de Venn.
Ejemplo de Unión de Conjuntos (∪)
Recordemos que la unión de conjuntos consiste en combinar o considerar todos los elementos que existan entre los conjuntos señalados, por ejemplo:
A = {1, 2, 3}
B = {3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5}Nota que el 3 se repite en ambos conjuntos, pero no es necesario repetirlo en la unión ya que en los conjuntos sólo se ponen los valores sin repetirlos.
Ejercicio: Dado los siguientes conjuntos, determina la unión:
A = {a, e, i, o, u}
B = {1, 2, 3, 4, 5}
C = {a, e, 3, 5, 6, z}
A ∪ B ∪ C = ?La respuesta es: A ∪ B ∪ C = {a, e, i, o, u, 1, 2, 3, 4, 5, 6, z} porque son los valores sin repetir en los 3 conjuntos. En un diagrama de Venn lo representamos como:
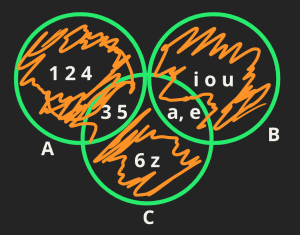
La parte sombreada por color naranja representa la unión de los conjuntos, nota que el conjunto A y B no no se sobre ponen porque no tienen elementos en común mientras que el conjunto C sí.
Ejemplo de Intersección de Conjuntos (∩)
La intersección de conjuntos consiste en identificar los elementos que existen en común entre conjuntos y se representa con el símbolo ∩. Por ejemplo:
A = {a, e, i, o, u}
B = {1, 2, 3, 4, 5}
C = {a, e, 3, 5, 6, z}
A ∩ B ∩ C = ?La respuesta es: A ∩ B ∩ C = {a, e, 3, 4} porque son los elementos que tienen en común C con A y B. Nota que A y B no tienen elementos en común. En diagrama de Venn se grafica como:
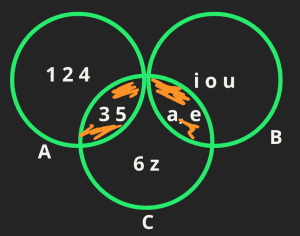
La parte sombreada con naranja representa la intersección de los conjuntos.
Ejemplo de Diferencia de Conjuntos ( – )
Calcula la diferencia entre los conjuntos A y B, donde:
A = {1, 2, 3, 4, 5}
B = {3, 4, 5, 6, 7}.Solución: Para calcular la diferencia entre dos conjuntos, necesitas eliminar los elementos comunes entre ellos del conjunto original. En este caso, queremos encontrar A – B.
Primero identifica los elementos que están presentes tanto en A como en B. En este caso, los elementos comunes son 3, 4 y 5.
Ahora, eliminas esos elementos de A. Entonces, A – B será igual a {1, 2}.
Por lo tanto, la diferencia entre los conjuntos A y B, A – B, es igual a {1, 2}.
Como resumen, la diferencia entre dos conjuntos A y B contiene todos los elementos que están en A pero no en B.
Ejemplo de Simetría o Diferencia Simétrica (Δ)
Calcula la diferencia simétrica entre los conjuntos A y B, donde:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}Solución: La diferencia simétrica de dos conjuntos, denotada como A Δ B, consiste en todos los elementos que están en A o en B, pero no en ambos conjuntos.
- Comenzamos identificando los elementos que están presentes tanto en A como en B. En este caso, los elementos comunes son 3 y 4.
- Luego, eliminamos esos elementos de A y B. Entonces, A Δ B será igual a {1, 2, 5, 6}.
Por lo tanto, la diferencia simétrica entre los conjuntos A y B, A Δ B, es igual a {1, 2, 5, 6}.
Recuerda que la diferencia simétrica de dos conjuntos contiene todos los elementos que están en uno de los conjuntos, pero no en ambos conjuntos al mismo tiempo.
Ejemplo de Complemento de un conjunto
Calcula el complemento del conjunto A en el conjunto universal U, donde:
U = {1, 2, 3, 4, 5}
A = {2, 4}Solución: El complemento de un conjunto A en el conjunto universal U, denotado como A’, consiste en todos los elementos que están en U pero no en A.
- Primero, identificamos todos los elementos que están en el conjunto universal U.
- Luego, eliminamos los elementos que están presentes en el conjunto A.
En este caso, el conjunto universal U es {1, 2, 3, 4, 5} y el conjunto A es {2, 4}.
- Por lo tanto, el complemento de A en U, A’, será igual a {1, 3, 5}.
Entonces, el complemento del conjunto A en el conjunto universal U, A’, es igual a {1, 3, 5}.
Recuerda que el complemento de un conjunto contiene todos los elementos que no están presentes en ese conjunto, pero sí están en el conjunto universal.
Teoría de conjuntos ejemplos resueltos paso a paso
Antes de comenzar los ejercicios y ejemplos de relaciones entre conjuntos, es importante que comprendas a qué se refiere exactamente este concepto.
Imagina que los conjuntos son grupos de amigos. Cada conjunto es como un grupo de personas que comparten algo en común. Ahora, una relación entre conjuntos es como una conexión especial que existe entre esos grupos de amigos.
Puedes pensar en una relación como una forma de mostrar cómo se relacionan los amigos de un grupo con los amigos de otro grupo. Por ejemplo, podríamos tener dos conjuntos: el conjunto A de niños que les gusta el fútbol y el conjunto B de niños que les gusta el baloncesto.
La relación entre estos conjuntos podría ser “juegan tanto fútbol como baloncesto juntos”. Esto significa que algunos niños del conjunto A también son amigos de algunos niños del conjunto B y disfrutan jugar juntos al fútbol o al baloncesto.
Ahora, si queremos visualizar esta relación, podríamos dibujar una línea o una flecha que conecte a los niños del conjunto A con los niños del conjunto B. Esto nos muestra que hay una conexión especial entre ellos.
Las relaciones entre conjuntos nos ayudan a entender cómo interactúan los elementos de un conjunto con los elementos de otro conjunto. Pueden ser de diferentes tipos, como “es mayor que”, “es amigo de”, “estudia con”, entre otros.
Ahora sí, empecemos a ver ejemplos un poco más avanzados.
Ejercicios y ejemplos de relaciones entre conjuntos
Ejemplo de Relación de Inclusión (⊂) y no Inclusión (⊄)
Considera los conjuntos A = {1, 2, 3} y B = {1, 2, 3, 4}. Determina si A está incluido en B y si B está incluido en A. Luego, determina si A no está incluido en B y si B no está incluido en A.
Solución:
- Relación de inclusión:
- Para determinar si A está incluido en B, verificamos si todos los elementos de A también están en B. En este caso, todos los elementos de A (1, 2 y 3) también están en B. Por lo tanto, A está incluido en B.
- Para determinar si B está incluido en A, verificamos si todos los elementos de B también están en A. En este caso, todos los elementos de B (1, 2, 3 y 4) también están en A. Por lo tanto, B está incluido en A.
- Relación de no inclusión:
- Para determinar si A no está incluido en B, buscamos al menos un elemento de A que no esté en B. En este caso, no hay ningún elemento en A que no esté en B. Por lo tanto, A está incluido en B y, por lo tanto, A no está no incluido en B.
- Para determinar si B no está incluido en A, buscamos al menos un elemento de B que no esté en A. En este caso, el elemento 4 está en B pero no en A. Por lo tanto, B no está incluido en A.
En resumen:
- A está incluido en B.
- B está incluido en A.
- A no está no incluido en B.
- B no está incluido en A.
Recuerda que la inclusión de conjuntos se refiere a si todos los elementos de un conjunto están presentes en otro conjunto. La no inclusión se produce cuando al menos un elemento de un conjunto no está presente en el otro conjunto.
Conjunto potencia, subconjuntos y subconjuntos propios
Ejemplo de potencia
Considera el conjunto A = {1, 2}. Encuentra el conjunto potencia de A, los subconjuntos de A y los subconjuntos propios de A.
Solución:
- Conjunto potencia de A: El conjunto potencia de A, denotado como P(A), consiste en todos los posibles subconjuntos de A, incluido el conjunto vacío.
Para encontrar el conjunto potencia de A, consideramos todos los subconjuntos posibles de A:
P(A) = { {}, {1}, {2}, {1, 2} }
Entonces, el conjunto potencia de A es P(A) = { {}, {1}, {2}, {1, 2} }.
- Subconjuntos de A: Los subconjuntos de A son todos los conjuntos que se pueden formar tomando algunos o todos los elementos de A, incluyendo el conjunto vacío.
Ejemplo de subconjunto
Los subconjuntos de A son:
{ } (conjunto vacío) {1} {2} {1, 2}
- Subconjuntos propios de A: Los subconjuntos propios de A son todos los subconjuntos de A, excepto A mismo. En otras palabras, son aquellos subconjuntos que contienen algunos elementos de A, pero no todos.
Los subconjuntos propios de A son:
{ } (conjunto vacío) {1} {2}
Recuerda que el conjunto vacío siempre es considerado un subconjunto de cualquier conjunto.
Teoría de conjuntos ejercicios resueltos de demostraciones
Ejemplo de demostración de un conjunto
Demuestra que la intersección de dos conjuntos A y B es igual a la intersección de B y A, es decir, A ∩ B = B ∩ A.
Solución: Para demostrar que la intersección de dos conjuntos A y B es igual a la intersección de B y A, debemos mostrar que ambos conjuntos contienen exactamente los mismos elementos.
Para hacer esto, utilizaremos la propiedad de igualdad de conjuntos, que establece que dos conjuntos son iguales si y solo si tienen los mismos elementos.
Demostración:
- Supongamos que x es un elemento arbitrario y consideremos la afirmación “x pertenece a A ∩ B”.
- Esto significa que x está presente tanto en A como en B. Por lo tanto, podemos decir que x pertenece a B y x pertenece a A. Esto se puede escribir como “x pertenece a B ∩ A”.
- Ahora, hemos demostrado que si x pertenece a A ∩ B, entonces x pertenece a B ∩ A.
- De manera similar, supongamos que y es un elemento arbitrario y consideremos la afirmación “y pertenece a B ∩ A”.
- Esto significa que y está presente tanto en B como en A. Por lo tanto, podemos decir que y pertenece a A y y pertenece a B. Esto se puede escribir como “y pertenece a A ∩ B”.
- Ahora, hemos demostrado que si y pertenece a B ∩ A, entonces y pertenece a A ∩ B.
- Dado que hemos demostrado que cualquier elemento que pertenece a A ∩ B también pertenece a B ∩ A, y viceversa, podemos concluir que A ∩ B = B ∩ A.
Por lo tanto, hemos demostrado que la intersección de dos conjuntos A y B es igual a la intersección de B y A, es decir, A ∩ B = B ∩ A.

