En este post vas a Aprender cómo pasar de hexadecimal a octal paso a paso y desde cero.
Para este ejercicio vas a pasar el número hexadecimal B9 a octal y lo haremos con una serie de pasos.
Pasos para pasar de Hexadecimal a Octal
- Convertir de hexadecimal a decimal.
- Pasar de decimal a binario.
- Convertir de binario a octal.
Convertir de hexadecimal a decimal
El primer paso es convertir dígito por dígito del hexadecimal a decimal. Por ejemplo, tenemos que en el sistema hexadecimal la letra A equivale a 10 en decimal y la letra B equivale a 11.

Quiere decir que podemos convertir la B a 11 en decimal. El número 9 en hexadecimal sigue siendo 9 en decimal por lo que lo podemos dejar igual.
Convertir de decimal a binario
El siguiente paso es pasar del decimal a binario. Podemos hacerlo también manteniendo los dígitos separados y convertir uno a uno.
Para eso te recomiendo colocar los resultados de las potencias de base 2, es decir, 8, 4, 2 y 1 porque 2 a la 0 es igual a 1, 2 a la 1 es igual a 2, 2 a la 2 igual a 4 y 2 al cubo es igual a 8.
Ahora lo único que tenemos que hacer es determinar qué combinaciones de cada dígito nos va a dar 9 como resultado.
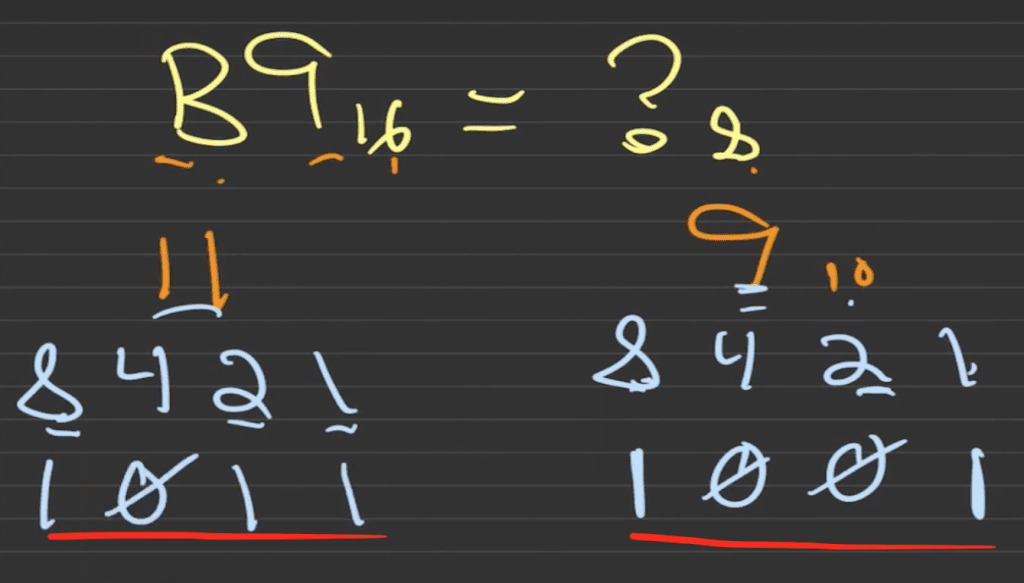
Por ejemplo, en este grupo de cuatro la combinación que me da 9 es 8 y 1 porque 8 + 1 es igual a 9. Como usé el 8 y el 1 les voy a poner un 1 y un 1 respectivamente. El 4 y 2 no los usé, entonces los voy a poner 0 y 0.
Vamos a hacer lo mismo para el 11. Si sumo 8+ 2 + 1 = 11, esos dígitos voy a poner un 1 respectivamente y 0 en el 4 porque no lo usé.
Ya hemos completado la conversión de decimal a binario.
Paso final para pasar de hexadecimal a octal
El siguiente paso es pasar de binario a octal y para eso podemos dividir el número binario por grupos de tres de derecha a izquierda.
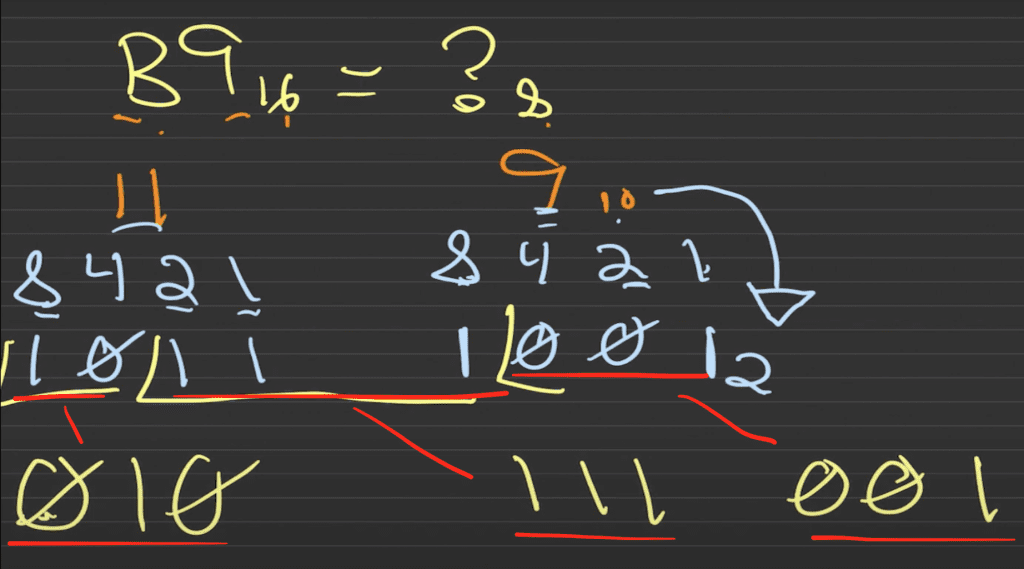
Queda como resultado de derecha a izquierda:
- 001
- 111
- 010
Como puedes ver, en el tercer grupo de 3 le puse un 0 al inicio por que sólo quedaban “10” y fue sólo por convención ya que realmente “010” y “10” son iguales, el 0 inicial es redundante pero lo he agregado para que todos sean grupos de 3.
Una vez separados, lo siguiente es colocar de nuevo las potencias de base 2 en cada grupo.
Lo único que tenemos que hacer ahora es multiplicar cada potencia por el dígito correspondiente y sumarlos.
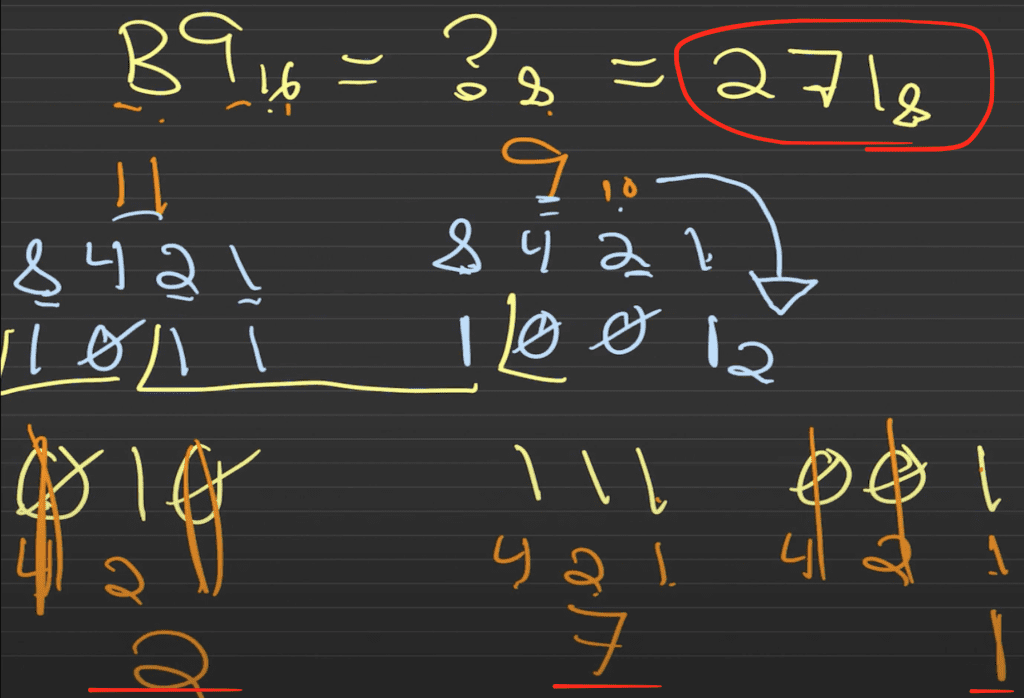
En este caso tenemos algunos ceros y todo número multiplicado por cero es cero. Por lo tanto, podemos ignorar y quitarlos.
En el primer grupo queda 1.
El segundo grupo de 111 tenemos podemos sumar 4 + 2 + 1 = 7.
Y en el tercer grupo Sólo queda el 2.
Y esta es la respuesta a la conversión de hexadecimal a octal. B9 en hexadecimal es igual a 271 en octal.
Han sido tres pasos de conversiones pero conforme practicas, más fácil e intuitivo se hace, esa es la clave para mejorar.
¿No quieres perderte los vídeos? ¡Suscríbete al canal de Youtube!
Entra para ver más guías y materiales sobre conversión de sistemas numéricos y matemáticas discretas para programación e ingeniería de software.
Como complemento, conoce más sobre el significado de hexadecimal.