En este post vas a Aprender cómo pasar de octal a hexadecimal con una serie de pasos explicados a detalle y de manera sencilla.
Para este ejercicio vas a convertir el número octal 271 a su equivalente en hexadecimal.
Como pasar de octal a hexadecimal pasos a seguir
Para convertir del sistema octal a hexadecimal vas a seguir estos pasos:
- Primero convertir de octal a binario, dígito por dígito.
- Después vas a convertir de binario a decimal.
- Finalmente, de decimal lo convertimos a hexadecimal.
Convertir de sistema octal a binario
Comencemos a convertir el número octal a binario. Para hacerlo, vas a separar dígito por dígito (es decir, 2, 7 y 1 en este ejemplo) y cada uno lo convertirás a binario.
Ahora para convertir a binario es muy sencillo, solamente necesitas colocar las potencias de dos consecutivamente.
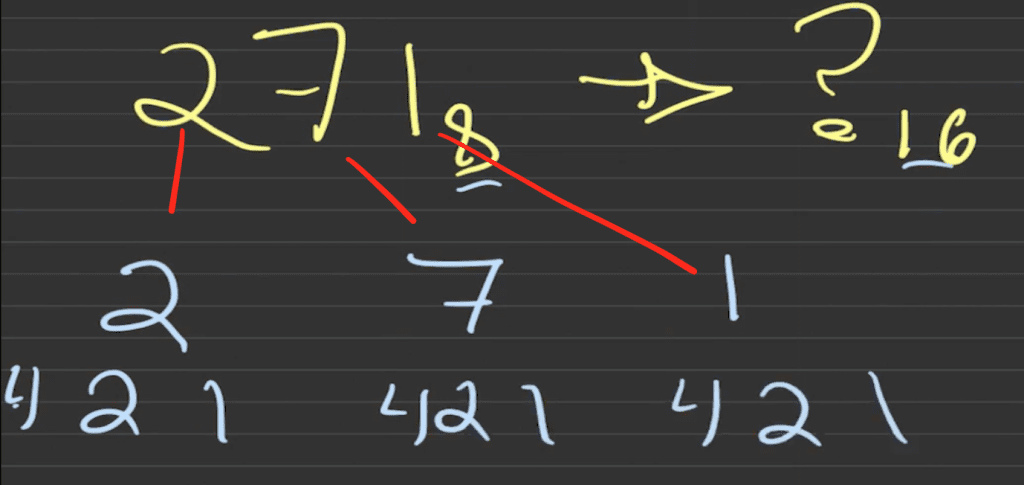
Ahora sólo hay que ver cómo obtenemos el valor octal usando la combinación de los resultados de las potencias de dos.
Para el primer dígito (el 2) existe por sí mismo como resultado de potencia de 2 a la 1, entonces puedes colocar en esa posición un 1 y 0 en las restantes.
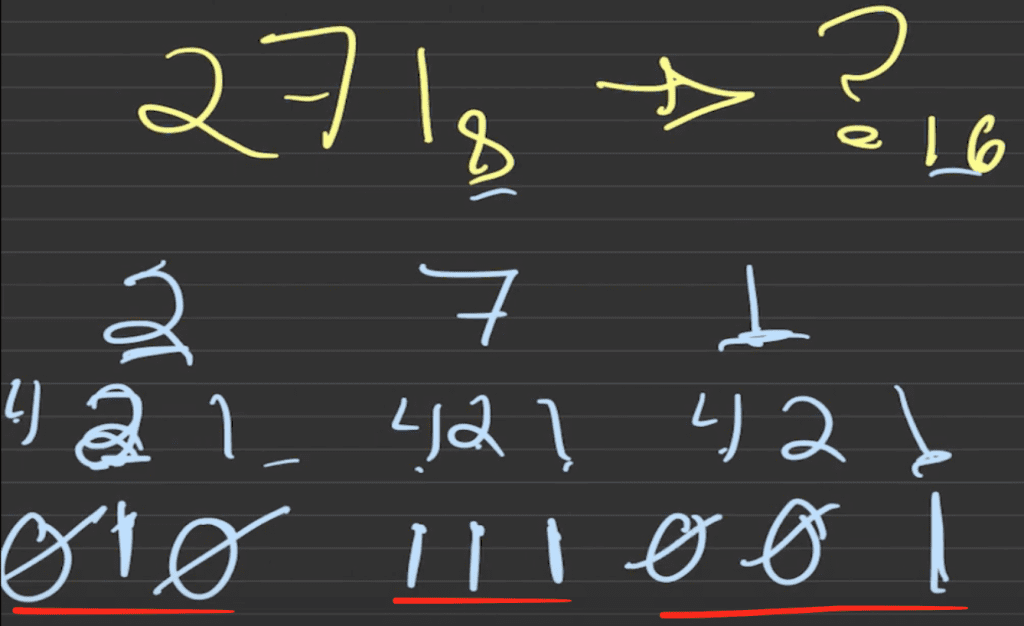
Para el 7 necesitas pensar cómo puedes obtenerlo. En este caso, podemos sumar 4 + 2 + 1 = 7.
Ya que usamos los 3 valores, entonces puedes colocar un uno en cada posición respectiva, es decir, 111.
Ahora, para obtener el 1 es sencillo, existe el uno por sí mismo como resultado de 2 elevado a la 0, aparte de que 1 en binario es igual a 1 en octal. Quiere decir que vas a poner el uno como no usaste las otras potencias, entonces les colocas 0.
Hasta aquí ya tenemos del sistema octal a binario, ahora vamos a convertir de binario a decimal.
Convertir de sistema binario a decimal
Para convertir de binario a decimal necesitas dividir los números binarios en grupos de 4 dígitos. En este ejemplo, quedan como: 1011 y 1001.
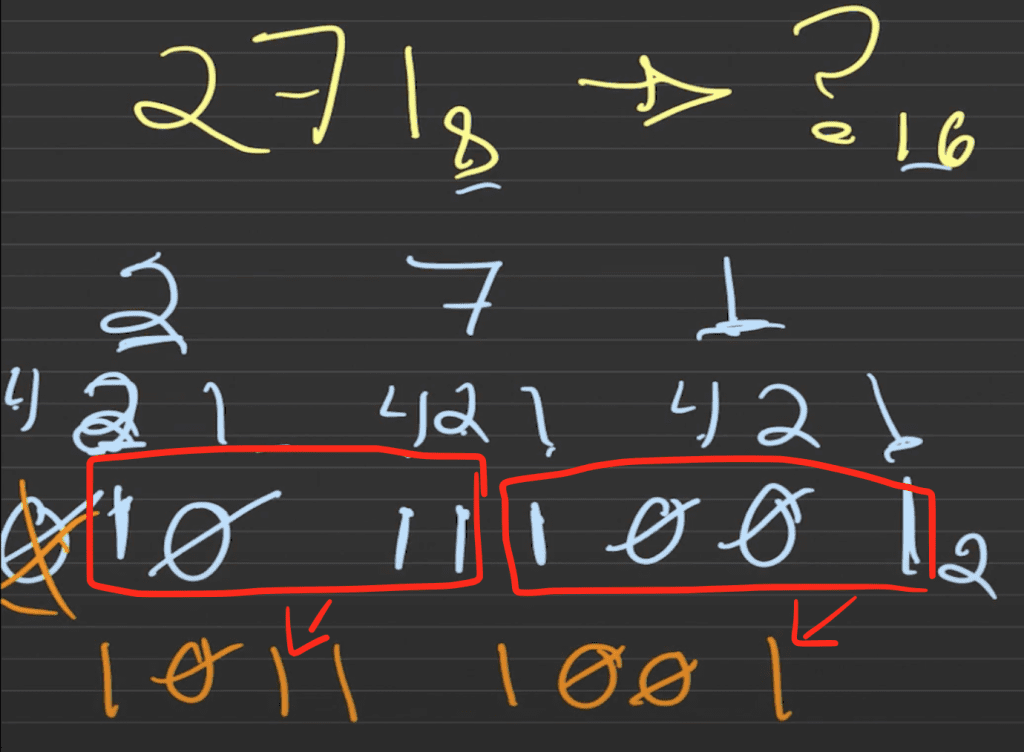
Algo importante a destacar es que toda cantidad que tenga un cero al inicio, el 0 es redundante y puede ser descartado. Por ejemplo, 271 0271. Entonces si queda un cero al inicio, lo puedes quitar.
Ahora vamos a convertir estos valores binarios a decimal.
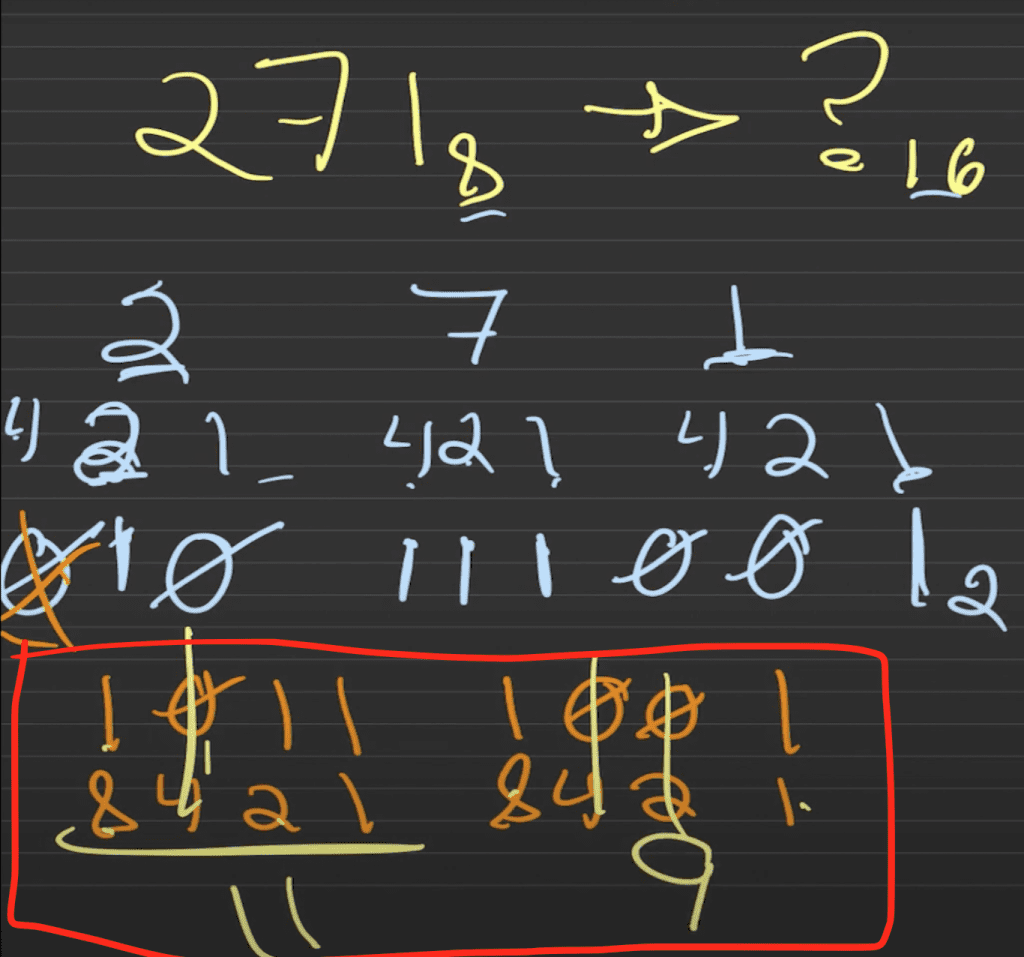
Por comodidad, si quieres puedes poner otra vez los resultados de las potencias de base (8, 4, 2 y 1).
Lo único que tienes que hacer es convertir multiplicando cada resultado de la potencia por el dígito correspondiente y los que tienen ceros como todo el número multiplicado por cero es cero pues los puedes ignorar porque no los vas a usar.
Después vamos a sumar el resultado de las multiplicaciones. Sé que suena un poco confuso pero no te preocupes, vas a ver que es muy sencillo.
Esto equivale a decir que vamos a suma r8 + 2 + 1 = 11 para el primer grupo y 8 + 1 = 9 para el segundo grupo.
Convertir de sistema decimal a hexadecimal
Para finalizar, necesitas convertir de decimal a hexadecimal ya con los números decimales en mano sólo tenemos que pasarlos a hexadecimal.
En hexadecimal, A equivale a 10 decimal y B equivale a 11.
En este ejemplo tenemos un 11, por lo tanto, lo convertimos a B. El 9 en decimal sigue siendo 9 en hexadecimal, por lo que lo dejamos igual.
La respuesta final es que 271 en sistema octal equivale a B9 en sistema hexadecimal.
¿No quieres perderte los vídeos? ¡Suscríbete al canal de Youtube!
Entra para ver más guías y materiales sobre conversión de sistemas numéricos y matemáticas discretas para programación e ingeniería de software.
Como complemento, conoce más sobre el significado de hexadecimal.
